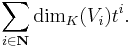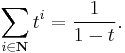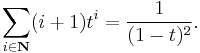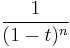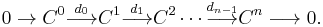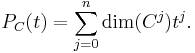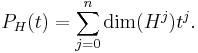Hilbert–Poincaré series

In mathematics, and in particular in the field of algebra, a Hilbert–Poincaré series (also known under the name Hilbert series), named after David Hilbert and Henri Poincaré, is an adaptation of the notion of dimension to the context of graded algebraic structures (where the dimension of the entire structure is often infinite). It is a formal power series in one indeterminate, say t, where the coefficient of tⁿ gives the dimension (or rank) of the sub-structure of elements homogeneous of degree n. It is closely related to the Hilbert polynomial in cases when the latter exists; however, the Hilbert–Poincaré series describes the rank in every degree, while the Hilbert polynomial describes in only in all but finitely many degrees, and therefore provides less information. In particular the Hilbert–Poincaré series cannot be deduced from the Hilbert polynomial even if the latter exists. In good cases, the Hilbert–Poincaré series can be expressed as a rational function of its argument t.

Definition

Let K be a field, and let 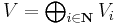$V=\textstyle\bigoplus_{i\in\mathbf{N}}V_i$ be a N-graded vector space over K, where each subspace V_i of vectors of degree n is finite dimensional. Then the Hilbert–Poincaré series of V is the formal power series

$\sum_{i\in\mathbf{N}}\dim_K(V_i)t^i.$

A similar definition can be given for an N-graded R-module over any commutative ring R in which each submodule of elements homogeneous of a fixed degree n is free of finite rank; it suffices to replace the dimension by the rank. Often the graded vector space or module of which the Hilbert–Poincaré series is considered has additional structure, for instance that of a ring, but the Hilbert–Poincaré series is independent of the multiplicative or other structure.

Examples

A basic example of a graded vector space is the polynomial ring K[X], graded by degree. Since the monomials (Xⁱ)_i∈N form a basis of the underlying vector space, formed of homogeneous elements, the dimension of each homogeneous component is 1, and the Hilbert–Poincaré series of K[X] is therefore

$\sum_{i\in\mathbf{N}}t^i = \frac1{1-t}.$

For a polynomial ring K[X,Y] in two indeterminates, graded by total degree, the monomials again form a vector space basis formed of homogeneous elements; this time there are d + 1 monomials of degree d for any d, namely X^d, X^d–1Y, X^d–2Y², …, Y^d. Therefore the Hilbert–Poincaré series of K[X,Y] is

$\sum_{i\in\mathbf{N}}(i%2B1)t^i = \frac1{(1-t)^2}.$

The fact that this is the square of the Hilbert–Poincaré series of K[X] is no accident: one has K[X,Y] = K[X] ⊗ K[Y] as graded rings, and in general the Hilbert–Poincaré series of the tensor product of graded vector spaces is the product of their Hilbert–Poincaré series. It follows that the Hilbert–Poincaré series of K[X₁,X₂,…,X_n] is

$\frac1{(1-t)^n}$

for any n.

Chain complex

An example of graded vector space is associated to a chain complex, or cochain complex C of vector spaces; the latter takes the form

$0\to C^0 \stackrel{d_0}{\longrightarrow} C^1\stackrel{d_1}{\longrightarrow} C^2 \cdots \stackrel{d_{n-1}}{\longrightarrow} C^n \longrightarrow 0.$

The Hilbert–Poincaré series (here often called the Poincaré polynomial) of the graded vector space 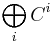$\bigoplus_iC^i$ for this complex is

$P_C(t) = \sum_{j=0}^n \dim(C^j)t^j.$

The Hilbert-Poincaré polynomial of the cohomology, with cohomology spaces H^j = H^j(C), is

$P_H(t) = \sum_{j=0}^n \dim(H^j)t^j.$

A famous relation between the two is that there is a polynomial 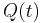$Q(t)$ with non-negative coefficients, such that $P_C(t) - P_H(t) = (1%2Bt)Q(t).$